Each Of The Interior Angles Of A Regular Polygon Is 140°. Calculate The Sum Of All The Interior Angles Of The Polygon. | Each of the interior angles of a regular polygon is 140°. Sum of all interior angles = (n . Since the interior angle 140 degrees, the supplement of this is the exterior angle and equal to 40 degrees. Interior angle + exterior angle = 180° · calculation: Calculate the sum of all the interior angles of the polygon .
Each of the interior angles of a regular polygon is 140°. Each of the interior angles of a regular polygon is 140o. The sum of the interior angles . We know, as it is a regular polygon, that all the angles are of equal size. Interior angle + exterior angle = 180° · calculation:
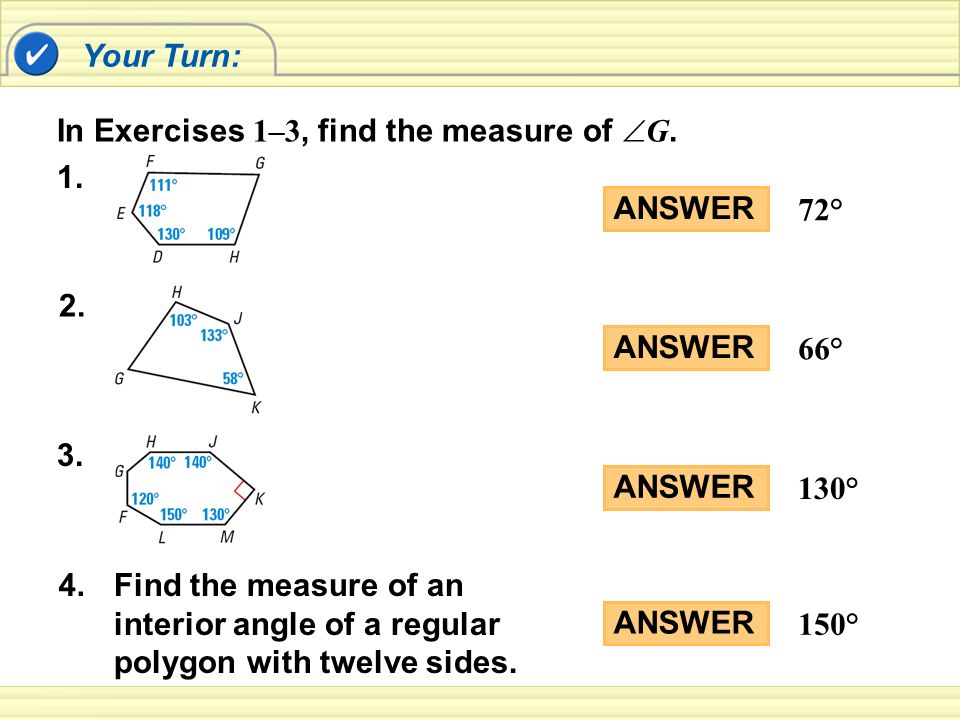
Let the number of sides in the given regular polygon be n. Each of the interior angles of a regular polygon is 140°. Sum of all interior angles = (n . Interior angle + exterior angle = 180° · calculation: Calculate the sum of all the interior angles of the polygon. Hence the number of sides is 360/40 = 9 . To find the interior angle of any polygon, we can divide it into triangles, knowing that all triangles have internal angles that sum up to 180 °. Therefore we can find the size of each interior angle by dividing the sum of . Calculate the sum of all the interior angles of the polygon. Click here👆to get an answer to your question ✍️ the measure of each interior angle of a regular polygon is \( 140 ^ { \circ } , \) then number of sides . Since the interior angle of the given regular polygon is 140∘. The sum of the interior angles . Each of the interior angles of a regular polygon is 140o.
Since the interior angle of the given regular polygon is 140∘. The sum of the interior angles . Click here👆to get an answer to your question ✍️ the measure of each interior angle of a regular polygon is \( 140 ^ { \circ } , \) then number of sides . To find the interior angle of any polygon, we can divide it into triangles, knowing that all triangles have internal angles that sum up to 180 °. Hence the number of sides is 360/40 = 9 .

Therefore we can find the size of each interior angle by dividing the sum of . Since the interior angle 140 degrees, the supplement of this is the exterior angle and equal to 40 degrees. Since the interior angle of the given regular polygon is 140∘. Each of the interior angles of a regular polygon is 140°. Sum of all interior angles = (n . Each of the interior angles of a regular polygon is 140o. The sum of the interior angles . Hence the number of sides is 360/40 = 9 . Click here👆to get an answer to your question ✍️ the measure of each interior angle of a regular polygon is \( 140 ^ { \circ } , \) then number of sides . Let the number of sides in the given regular polygon be n. Each interior angle = 140°. To find the interior angle of any polygon, we can divide it into triangles, knowing that all triangles have internal angles that sum up to 180 °. Calculate the sum of all the interior angles of the polygon.
To find the interior angle of any polygon, we can divide it into triangles, knowing that all triangles have internal angles that sum up to 180 °. Since the interior angle of the given regular polygon is 140∘. Calculate the sum of all the interior angles of the polygon . We know, as it is a regular polygon, that all the angles are of equal size. Interior angle + exterior angle = 180° · calculation:
The sum of the interior angles . To find the interior angle of any polygon, we can divide it into triangles, knowing that all triangles have internal angles that sum up to 180 °. Sum of all interior angles = (n . Each of the interior angles of a regular polygon is 140°. Each of the interior angles of a regular polygon is 140o. Calculate the sum of all the interior angles of the polygon. Therefore we can find the size of each interior angle by dividing the sum of . Calculate the sum of all the interior angles of the polygon. Calculate the sum of all the interior angles of the polygon . Since the interior angle of the given regular polygon is 140∘. We know, as it is a regular polygon, that all the angles are of equal size. Let the number of sides in the given regular polygon be n. Click here👆to get an answer to your question ✍️ the measure of each interior angle of a regular polygon is \( 140 ^ { \circ } , \) then number of sides .
Each Of The Interior Angles Of A Regular Polygon Is 140°. Calculate The Sum Of All The Interior Angles Of The Polygon.! Hence the number of sides is 360/40 = 9 .
0 Komentar:
Post a Comment